Jasper Tan, Daniel LeJeune, Blake Mason, Hamid Javadi, Richard G. Baraniuk, "Benign Overparameterization in Membership Inference with Early Stopping", arXiv:2205.14055.

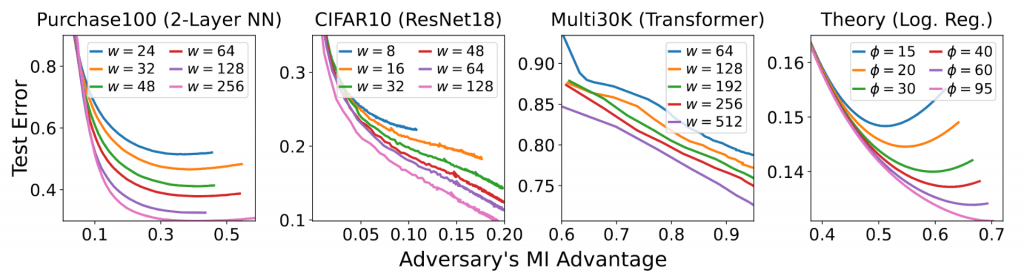
Does a neural network's privacy have to be at odds with its accuracy? In this work, we study the effects the number of training epochs and parameters have on a neural network's vulnerability to membership inference (MI) attacks, which aim to extract potentially private information about the training data. We first demonstrate how the number of training epochs and parameters individually induce a privacy-utility trade-off: more of either improves generalization performance at the expense of lower privacy. However, remarkably, we also show that jointly tuning both can eliminate this privacy-utility trade-off. Specifically, with careful tuning of the number of training epochs, more overparameterization can increase model privacy for fixed generalization error. To better understand these phenomena theoretically, we develop a powerful new leave-one-out analysis tool to study the asymptotic behavior of linear classifiers and apply it to characterize the sample-specific loss threshold MI attack in high-dimensional logistic regression. For practitioners, we introduce a low-overhead procedure to estimate MI risk and tune the number of training epochs to guard against MI attacks.