Abstract:
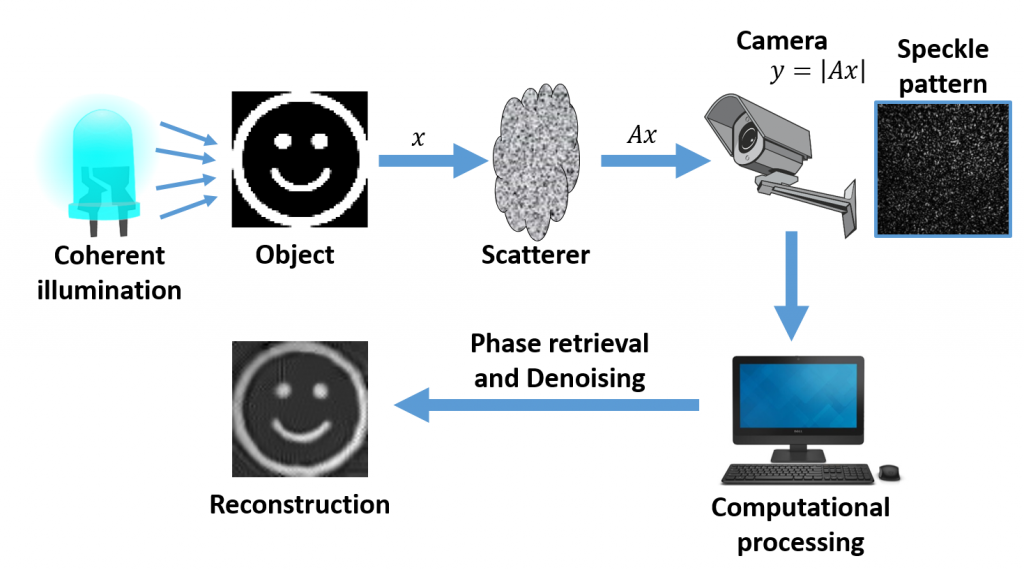
A transmission matrix describes the input-output relationship of a complex wavefront as it passes through/reflects off a multiple-scattering medium, such as frosted glass or a painted wall. Knowing a medium's transmission matrix enables one to image through the medium, send signals through the medium, or even use the medium as a lens. The double phase retrieval method is a recently proposed technique to learn a medium's transmission matrix that avoids difficult-to-capture interferometric measurements. Unfortunately, to perform high resolution imaging, existing double phase retrieval methods require (1) a large number of measurements and (2) an unreasonable amount of computation.
In this work we focus on the latter of these two problems and reduce computation times with two distinct methods: First, we develop a new phase retrieval algorithm that is significantly faster than existing methods, especially when used with an amplitude-only spatial light modulator (SLM). Second, we calibrate the system using a phase-only SLM, rather than an amplitude-only SLM which was used in previous double phase retrieval experiments. This seemingly trivial change enables us to use a far faster class of phase retrieval algorithms. As a result of these advances, we achieve a $100\times$ reduction in computation times, thereby allowing us to image through scattering media at state-of-the-art resolutions. In addition to these advances, we also release the first publicly available transmission matrix dataset. This contribution will enable phase retrieval researchers to apply their algorithms to real data. Of particular interest to this community, our measurement vectors are naturally i.i.d.~subgaussian, i.e., no coded diffraction pattern is required.
Dataset:
A public dataset containing the transmission matrices of various scattering media can be downloaded here.
Algorithm:
The prVAMP algorithm and a simple demo can be found within the phase directory of the Gampmatlab toolbox.
Paper:
This work is described in our paper here.